Air Propulsion Simulation

Simulating the performace of an air propulsion system as an alternative to solid rocket motors.

Boilerplate intro about why all of this was done

Show code

using Plots
plotly()
theme(:ggplot2); # In true R spirit

using Unitful
using DataFrames
using Measurements
using Measurements: value, uncertainty

This code is just the setup, using values scraped from various parts of the world wide web.

# Tank https://www.amazon.com/Empire-Paintball-BASICS-Pressure-Compressed/dp/B07B6M48SR/
V = (85 ± 5)u"inch^3"
P0 = (4200.0 ± 300)u"psi"
Wtank = (2.3 ± 0.2)u"lb"
Pmax = (250 ± 50)u"psi" # Max Pressure that can come out the nozzle

Wsolenoid = 1.5u"kg"

# Params
d_nozzle = ((1 // 18) ± 0.001)u"inch"
a_nozzle = (pi / 4) * d_nozzle^2

# Universal Stuff
P_amb = (1 ± 0.2)u"atm"
γ = 1.4 ± 0.05
R = 287.05u"J/(kg * K)"
T = (300 ± 20)u"K"

This is the actual simulation. Maybe throw some references in and explain some equations.

The rocket equation is pretty sick:

\[T = \dot{m} \cdot v_\text{Exit} + A_\text{Nozzle} \cdot (P - P_\text{Ambient}) \] And thats about all you need to get to the moon(Curtis 2020).

let
t = 0.0u"s"
P = P0 |> u"Pa"
M = V * (P / (R * T)) |> u"kg"
ts = 1u"ms"
global df = DataFrame(Thrust=(0 ± 0)u"N", Pressure=P0, Time=0.0u"s", Mass=M)
  while M > 0.005u"kg"
      # while t < 30u"s"
      # Calculate what is leaving tank
      P = minimum([P, Pmax])
      ve = sqrt((2 * γ / (γ - 1)) * R * T * (1 - P_amb / P)^((γ - 1) / γ)) |> u"m/s"
      ρ = P / (R * T) |> u"kg/m^3"
      ṁ = ρ * a_nozzle * ve |> u"kg/s"
  
      Thrust = ṁ * ve + a_nozzle * (P - P_amb) |> u"N"
  
      # Calculate what is still in the tank
      M = M - ṁ * ts |> u"kg"
      P = (M * R * T) / V |> u"Pa"
      t = t + ts
  
      df_step = DataFrame(Thrust=Thrust, Pressure=P, Time=t, Mass=M)
      append!(df, df_step)
  end
end

Heres the results plotted. Notice the massive error once the tank starts running low.

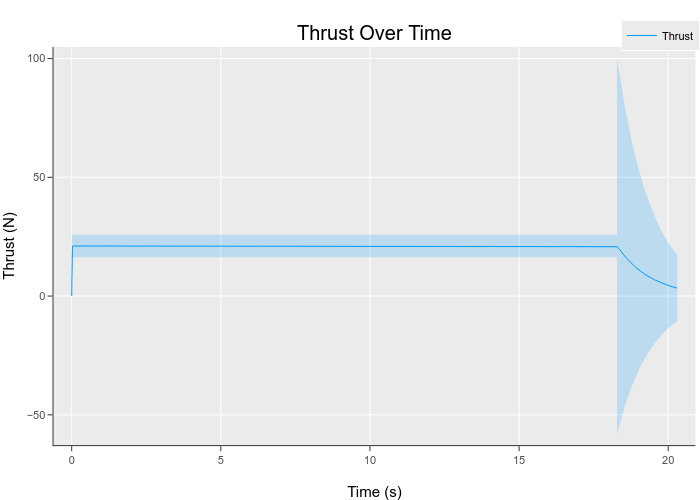
Big conclusion about things.